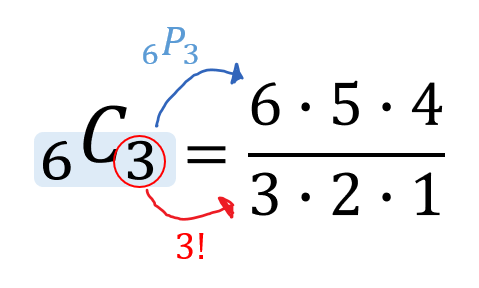
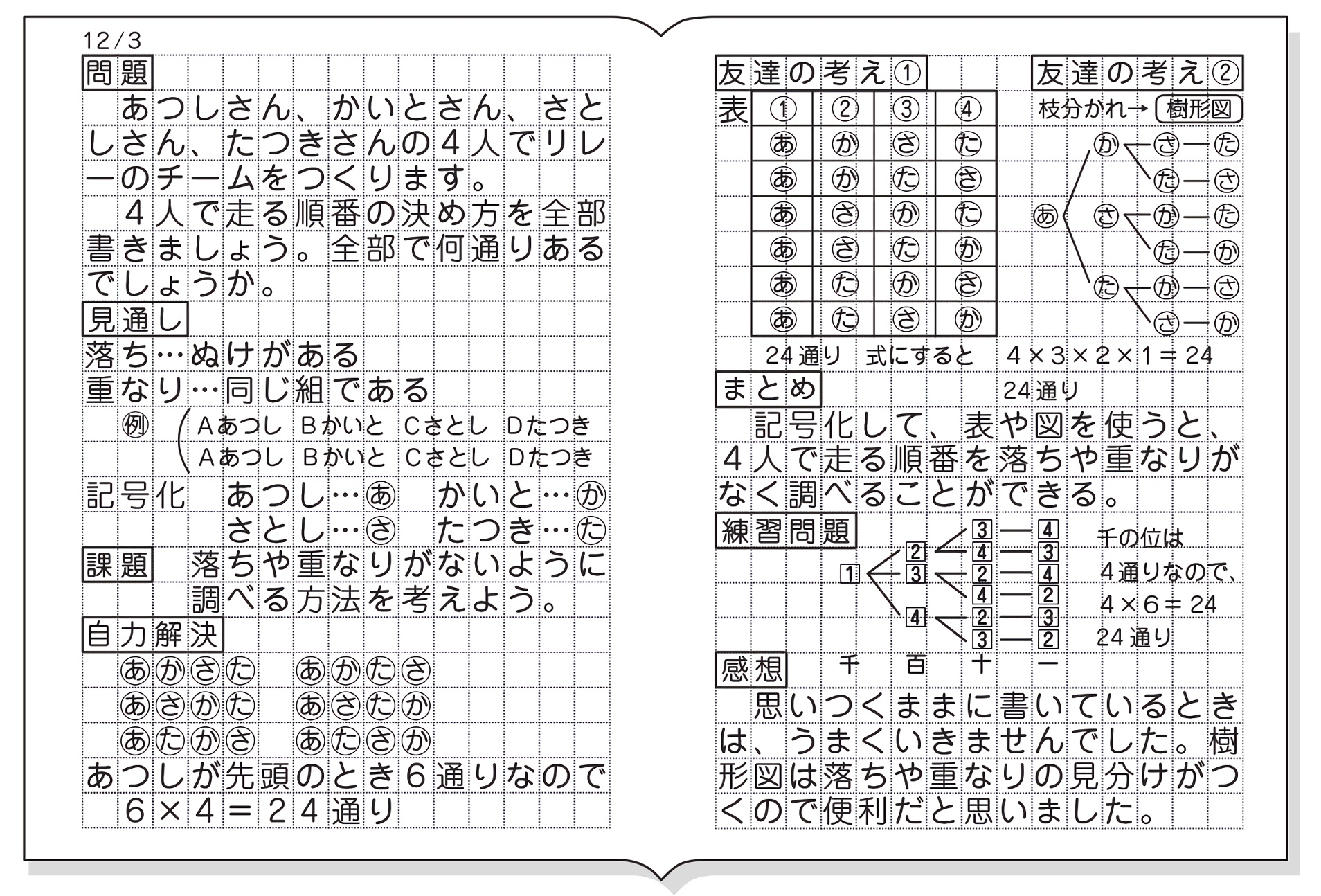
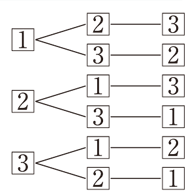
男子a、b、c、d、eの5人から3人を選ぶのはa-bとb-aを1通りとする場合の組み合わせ になるので、 5×4×3 3×2×1 =10通り。女子g、f、hの中から2人選ぶのは 3×2 2×1 =3通り。 男子5人から3人選んでから、女子3人から2人選ぶのは順列になるので、10×3=30通り。 解答 30通り 例題5 大小2つ
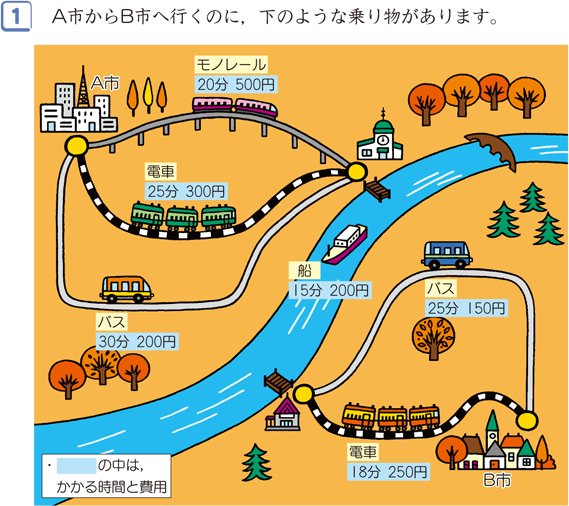
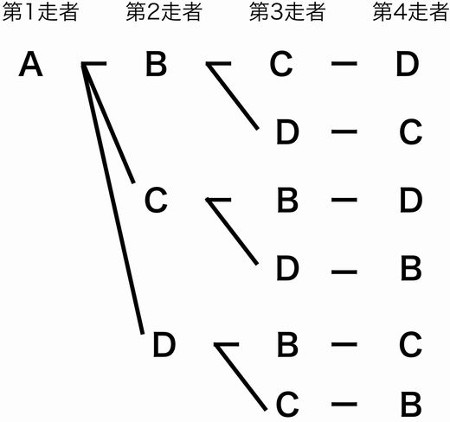
場合の数 組み合わせ 問題-ならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。ならない取り出し方の場合は組合せで考えればいいわけです。 では、問題を考えてみましょう。 1 (1)は「第1走者から第4走者までの4人を選ぶ・・・」 つまり、順序が問題になるので、『順列』の考えで。 4は「男子6人、女子10人の中から男子3人、女子4人
場合の数 組み合わせ 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「場合の数 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「場合の数 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「場合の数 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
 |  | |
「場合の数 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 | ||
「場合の数 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 | ||
「場合の数 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  | |
「場合の数 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 | 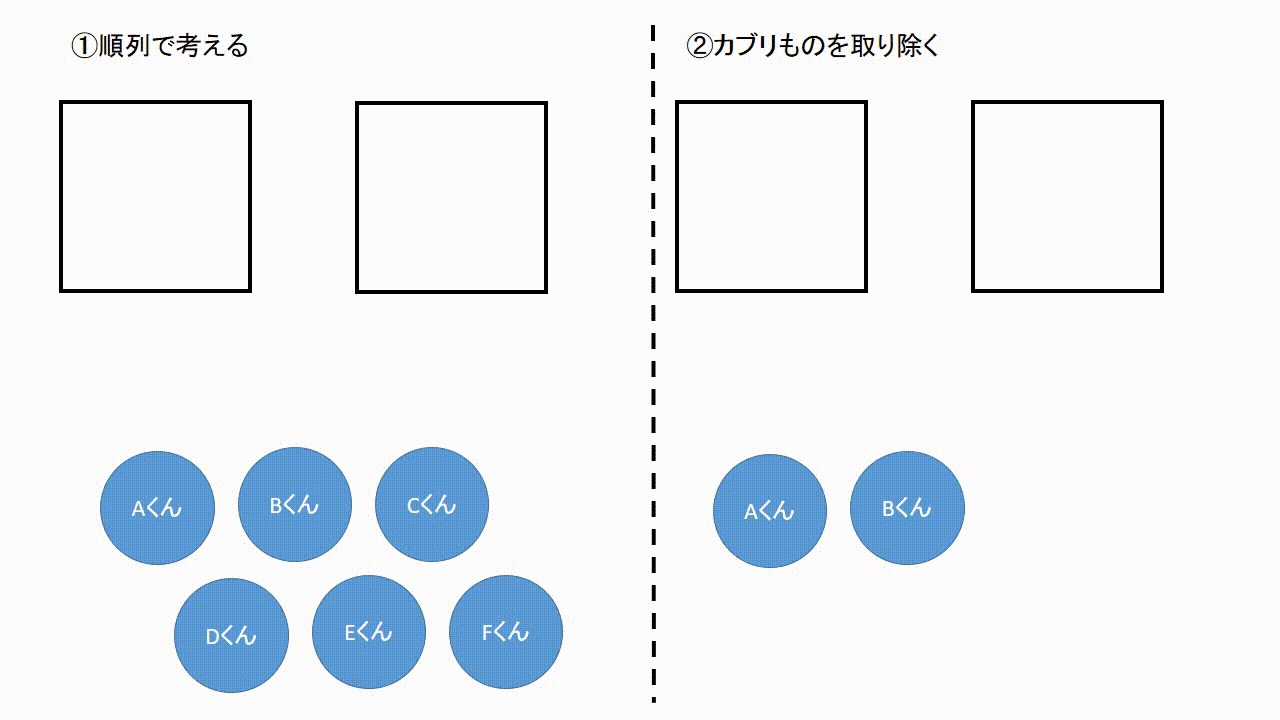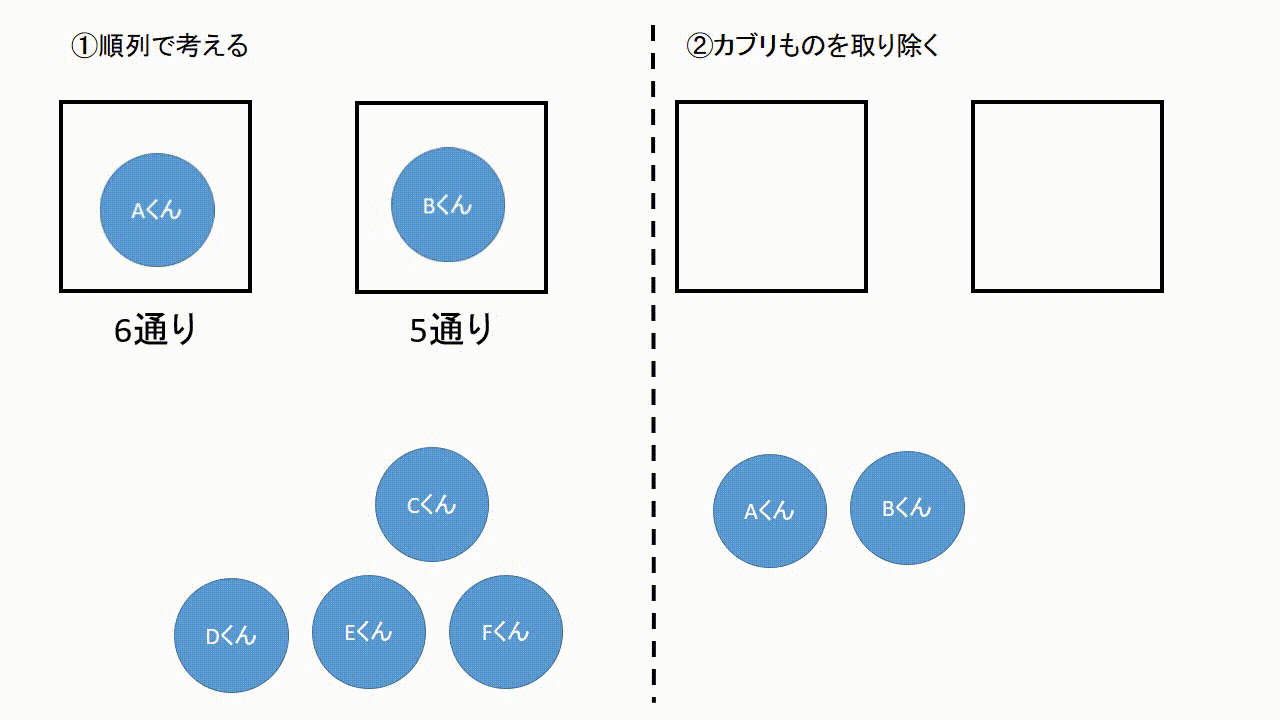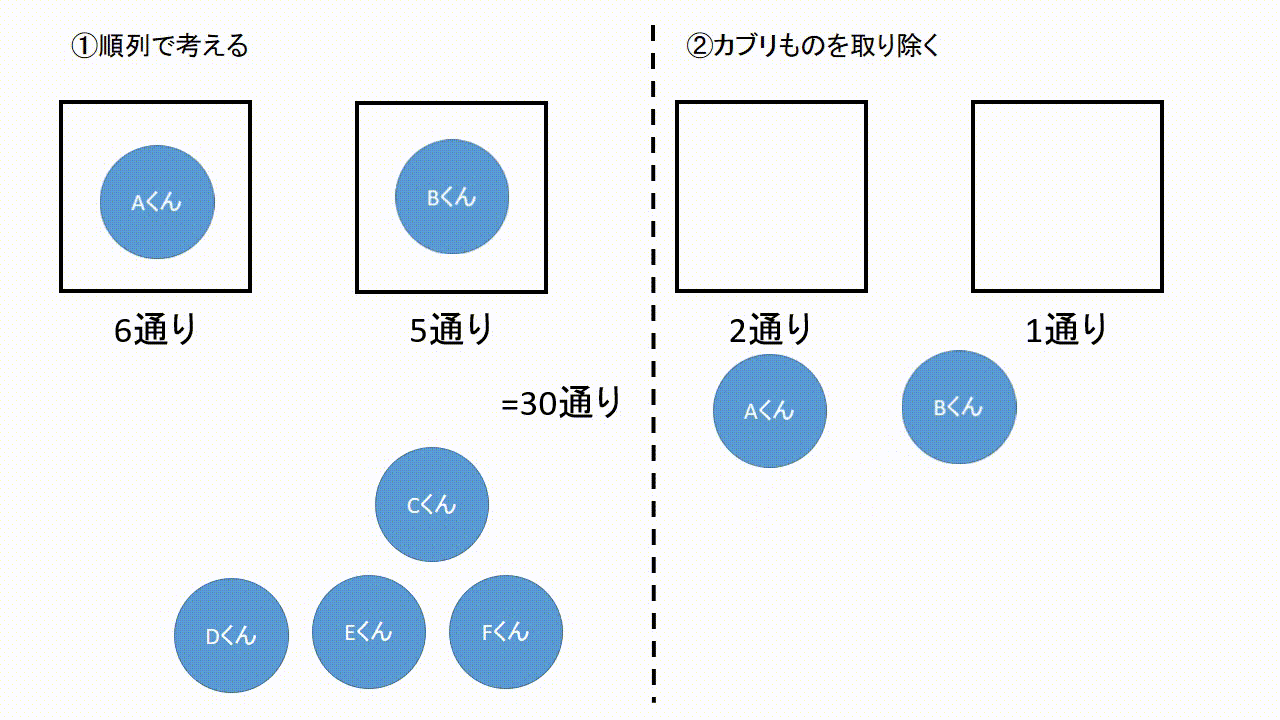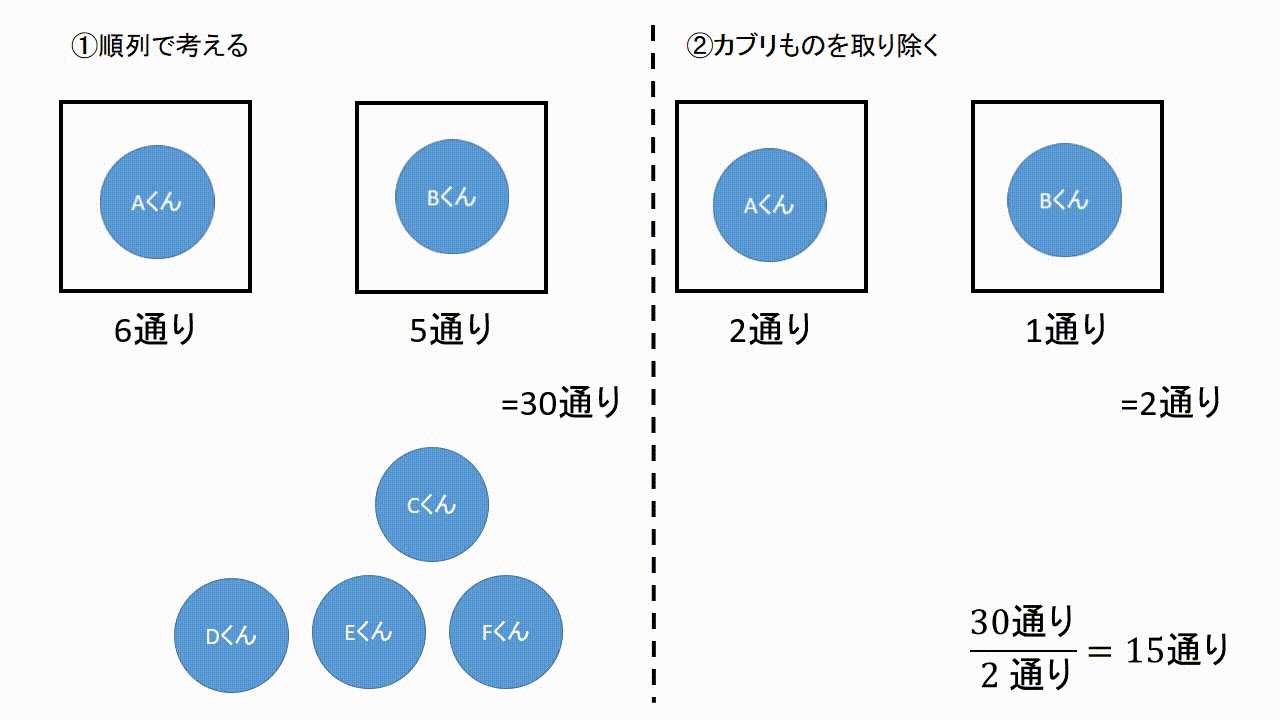 |  |
「場合の数 組み合わせ 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 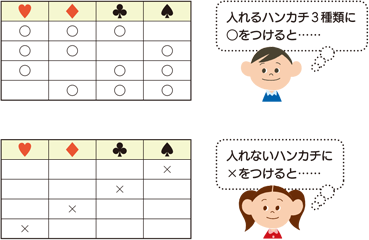 |
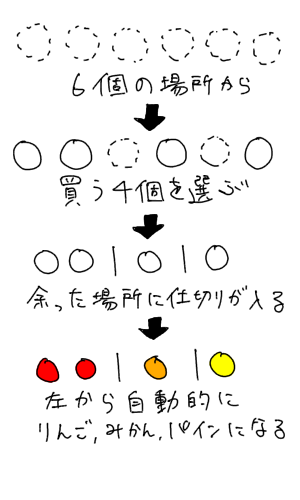 |  |  |
 |  |
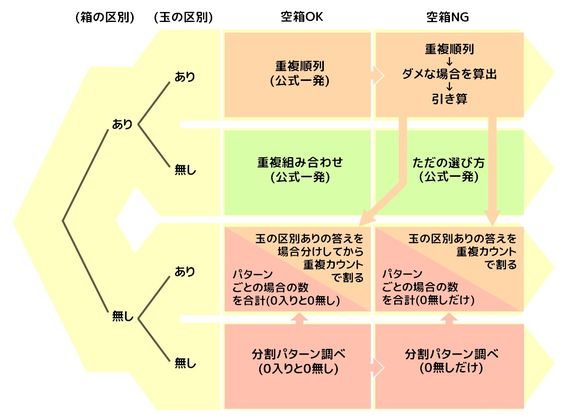
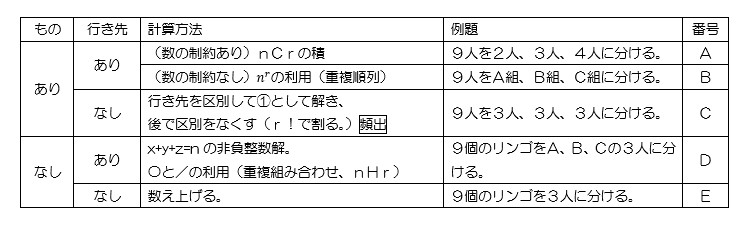
練習問題をダウンロードする 画像をクリックするとPDFファイルをダウンロード出来ます。 中学受験を成功させる 熊野孝哉の「場合の数」入試で差がつく51題 +13題改訂4版 (YELL books) 新品価格 ¥1,6 から (18/8/22 1921時点) (Visited 8,106 times, 1 visits today)この記事では,「A,B,Cの3文字から全部で7個選ぶ場合の数」のように,同じものがいくつかあってよい「重複組み合わせ」の考え方を説明します. 「重複組合せ」の問題設定としては 選ばれない色のボールがあっても良い場合 選ばれないボールがあっては
Incoming Term: 場合の数 組み合わせ 問題,




0 件のコメント:
コメントを投稿